If you would like to read previous articles in this series, please go to:
- Deploying Windows 7 – Part 1: Windows AIK 2.0 Enhancements
- Deploying Windows 7 – Part 2: Using DISM
- Deploying Windows 7 – Part 3: Understanding MAP 4.0
- Deploying Windows 7 – Part 5: MDT 2010 Enhancements
- Deploying Windows 7 – Part 6: Lite Touch using MDT 2010
- Deploying Windows 7 – Part 7: Automated LTI Deployment
- Deploying Windows 7 – Part 8: Understanding LTI Configuration Files
- Deploying Windows 7 – Part 9: Deploying 32-bit vs. 64-bit Windows
- Deploying Windows 7 – Part 10: Capturing and Deploying an Image of a Reference Computer
- Deploying Windows 7 – Part 11: Capturing an Existing Installation
- Deploying Windows 7 – Part 12: Planning for Application Compatibility
- Deploying Windows 7 – Part 13: Manual Migration from Windows XP to Windows 7
- Deploying Windows 7 – Part 14: Automated Migration from Windows XP to Windows 7
- Deploying Windows 7 – Part 15: Configuring the MDT Database
- Deploying Windows 7 – Part 16: Using the MDT Database
- Deploying Windows 7 – Part 17: Deploying Applications Based on Make and Model
- Deploying Windows 7 – Part 18: Determining the UUID of a Computer
- Deploying Windows 7 – Part 19: Building a Custom WinPE Tools CD
- Deploying Windows 7 – Part 20: Securing MDT (Part 1)
- Deploying Windows 7 – Part 21: Securing MDT (Part 2)
- Deploying Windows 7 – Part 22: Bulk Populating the MDT Database Using PowerShell
- Deploying Windows 7 – Part 23: Managing Drivers – Introduction
- Deploying Windows 7 – Part 24: Managing Drivers – Issues and Approaches
- Deploying Windows 7 – Part 25: Managing Drivers – Selection Profiles
- Deploying Windows 7 – Part 26: Managing Drivers – By Make and Model
- Deploying Windows 7 – Part 27: Managing Drivers – Tips and Tricks
- Deploying Windows 7 – Part 28: Managing Software Updates
- Deploying Windows 7 – Part 29: Completing the LTI Deployment Infrastructure
In the previous article of this series we looked at what MAP 4.0 can be used for, how to install it, and the layout of the tool’s user interface. One of the uses of this tool is to assess whether your desktop computers are ready to migrate to Windows 7 Enterprise edition. Let us perform a sample walkthrough using this tool on a test-bed network.
Preparing to Run the Windows 7 Readiness Assessment
Before you use MAP to assess the readiness of your desktop computers for a migration to Windows 7, you need to make sure they can be assessed. The great thing about MAP is that it is agent less, which means that you do not need to deploy a software agent to each desktop machine that you want to assess. Instead of using agents, MAP uses Windows Management Instrumentation (WMI) to collect hardware devices and software information from the computers on your network. In order for WMI to be able to do this, your desktop computers must be configured to allow remote WMI queries. This means that you have to enable the Remote Administration and the File & Printer Sharing exceptions in Windows Firewall on all your desktop computers. You can use Group Policy to enable Windows Firewall exceptions in an Active Directory-based network (in a workgroup you have to do this manually on each computer). Also, in a domain environment, you need to run MAP on a computer on which you have logged on as a member of the Domain Admins security group (in a workgroup environment you need to provide MAP with local Administrator credentials for each computer). Additional configuration steps may need to be performed in order to prepare your desktop computers for assessment by MAP. For more information, see the Getting Started Guide for MAP 4.0, which is available from Start | All Programs | Microsoft Assessment and Planning Toolkit. Be sure also to review the MAP FAQ before using MAP.
Performing a Windows 7 Readiness Assessment
To perform your Windows 7 Readiness assessment, open the MAP console, select the Inventory and Assessment button at the bottom portion of the navigation pane, expand Discover and Readiness in the top portion of the navigation pane, and select Windows 7 Readiness (Figure 1):

Figure 1: Running a Windows 7 Readiness assessment using MAP 4.0
Click the Inventory and Assessment Wizard link in the right pane to launch the Inventory and Assessment Wizard. On the first page of this wizard you can specify which method(s) you would like to use in order to locate the computers on your network (Figure 2). The supported methods in MAP 4.0 include:
- Querying Active Directory for computer accounts in domains or OUs you specify
- Using Win32 LAN Manager APIs to query the Computer Browser service to find computers belonging to workgroups
- Importing a list of computer names (NetBIOS or FQDNs) from a text file
- Scanning a specified IP address range for computers
- Manually specifying computer names (NetBIOS or FQDNs) if you only have a few computers to assess
- Discover Windows virtual machines running on VMware servers
By default, Active Directory and Windows network protocols are used, but to keep things simple in this example, we will clear the second option and only query Active Directory.
Note:
Selecting different options on this page may result in additional wizard pages being displayed later on.
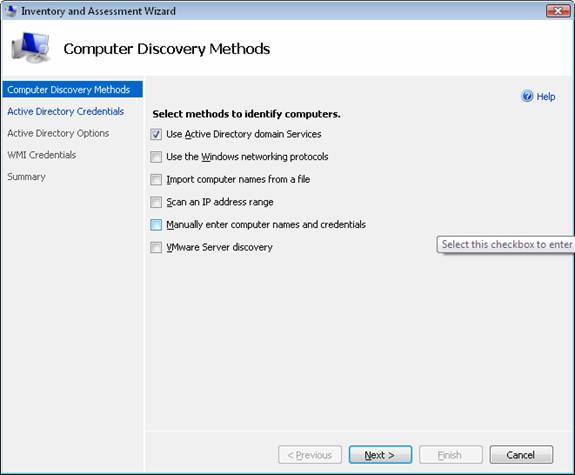
Figure 2: Choosing which methods to use to discover computers on your network
On the next page of the wizard we specify the Domain Admin credentials MAP can use to query Active Directory (Figure 3):

Figure 3: Specify Domain Admin credentials for MAP to query Active Directory
On the next wizard page, we will specify that MAP should only query for computer accounts in the Seattle Computers OU since those will be the computers we will pilot Windows 7 on (Figure 4):
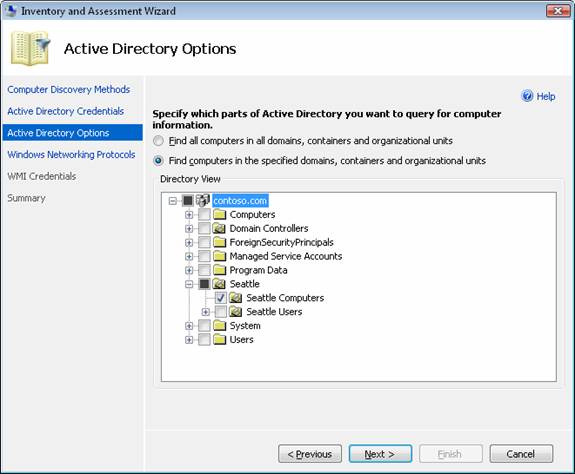
Figure 4: Specify the domain and organizational units where the computers reside
The next wizard page asks us for credentials MAP can use to remotely connect to each computer using WMI (Figure 5):
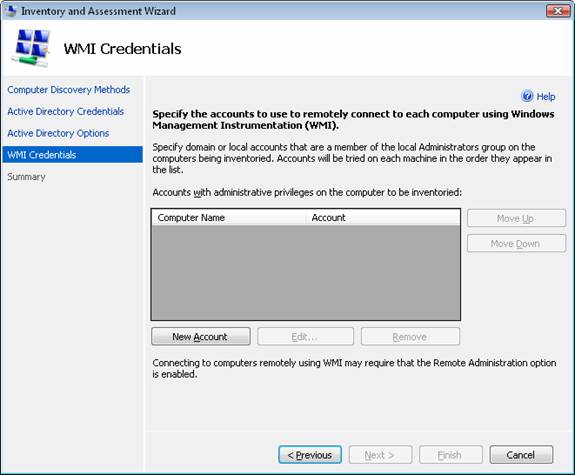
Figure 5: MAP needs credentials to remotely connect to computers using WMI
Clicking New Account opens the Inventory Account dialog box (Figure 6). Specify a Domain Admin account for the inventory account:

Figure 6: Specify a Domain Admin account for WMI connections to remote computers
Clicking Save adds the specified account to the WMI Credentials page of the wizard (Figure 7):
Figure 7: Credentials for remote WMI connections have been specified
The final page of the wizard summarizes the choices you have made (Figure 8):
Figure 8: Summary page of wizard
Clicking Finish starts the inventory process and displays a Status dialog box (Figure 9):
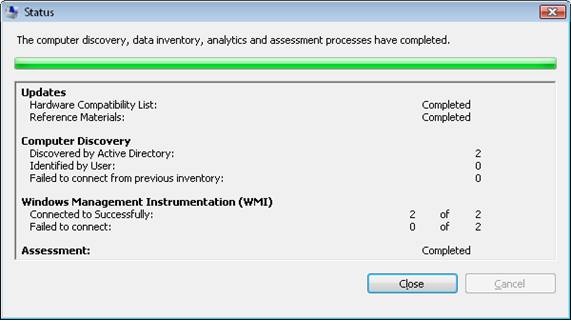
Figure 9: Status of the inventory process is displayed
Once the assessment is finished, click Close. After a few moments MAP will display the results of the assessment. Figure 10 shows that two client computers were found in the specified OU and that both of them were ready for Windows 7:
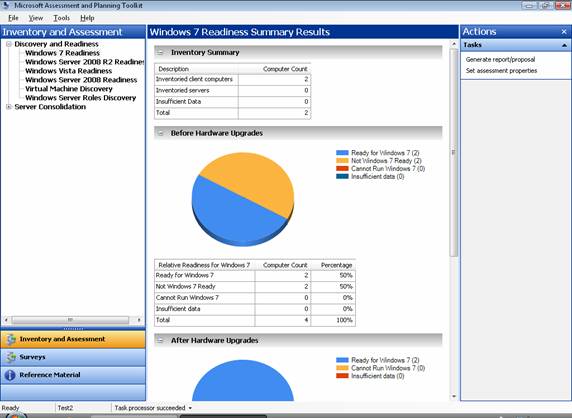
Figure 10: Summary results of the Windows 7 Readiness assessment
Scrolling down the middle pane of MAP shows additional details of the assessment. For instance, we can see in Figure 11 that there are a few device incompatibility issues that we will need to resolve with device manufacturers before we migrate the computers to Windows 7.
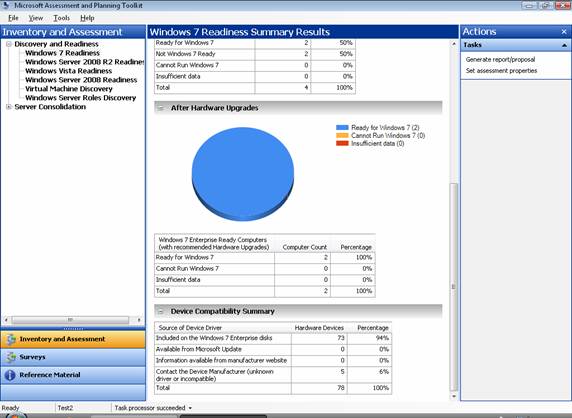
Figure 11: Note that 6% of the devices on the assessed computers may be incompatible with Windows 7
Changing the Hardware Requirements
Let us examine what hardware requirements were used during the above assessment as a basis for determining whether our computers are ready for Windows 7. In the Actions pane at the right side of the above figure, click Set Assessment Properties to open the Assessment Properties dialog box (Figure 12):
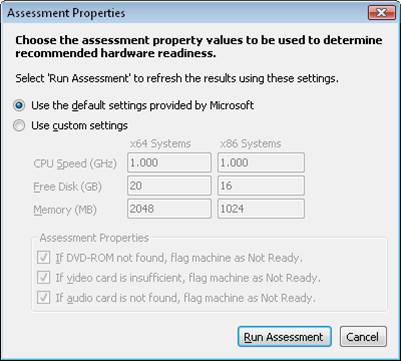
Figure 12: Default hardware values used by MAP for assessing Windows 7 readiness
By default, MAP uses the following minimum hardware requirements for Windows 7 readiness (these values are preliminary and are subject to change at RTM):
- CPU minimum speed 1.0 GHz
- Minimum free disk space 20 GB for x64 systems and 16 GB for x86 systems
- Minimum RAM of 2 GB for x64 systems and 1 GB for x86 systems
What if these hardware requirements are not sufficient for the needs of our business? For example, since we plan on using our two computers in Seattle for some fairly intensive work, such as video processing, let us increase these minimum requirements and see if our computers will still be ready for Windows 7. To do this, select Use Custom Settings and specify the new requirements shown in Figure 13:

Figure 13: Specifying more stringent hardware requirements for Windows 7
Now click Run Assessment to re-run the Windows 7 Readiness assessment using these more stringent hardware requirements (Figure 14):
Figure 14: Re-running the assessment
Generating Proposals and Reports
We have now run two assessments that basically answer the following two questions:
- How many computers at Seattle are ready for Windows 7?
- Will these computers still be ready for Windows 7 given our more stringent hardware requirements?
Let us generate reports we can share and review with our IT team and later with management. To generate reports, click Generate Report/Proposal in the Action pane at the right of Figure 11 shown previously. When you do this, MAP generates a proposal (Word doc) and an Excel workbook containing various reports (Figure 15):
Figure 15: Reports and proposals are being generated
Let us look at the Excel workbook first as it contains the detailed information our IT staff will need to review. To find our proposals and reports, select View | Saved Reports and Proposals to open the folder where the proposals and reports are found (Figure 16):
Figure 16: Proposals and Reports generated by MAP
We will open the Excel workbook and look at each worksheet. The first worksheet provides a summary of Windows 7 readiness information for computers that are already running a Microsoft Windows client (Figure 17):
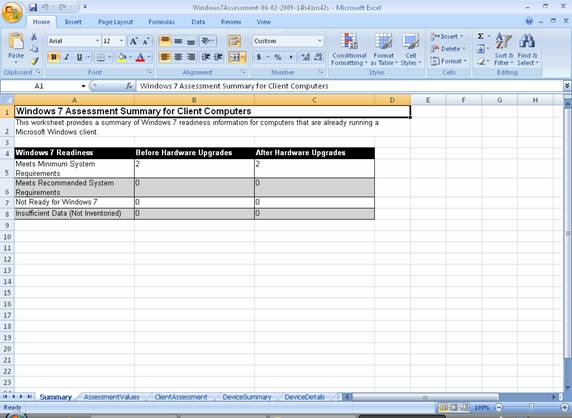
Figure 17: Windows 7 Assessment Summary for Client Computers worksheet
The next worksheet shows the system requirements provided by Microsoft in addition to any recommended settings that were used in the assessment (Figure 18):
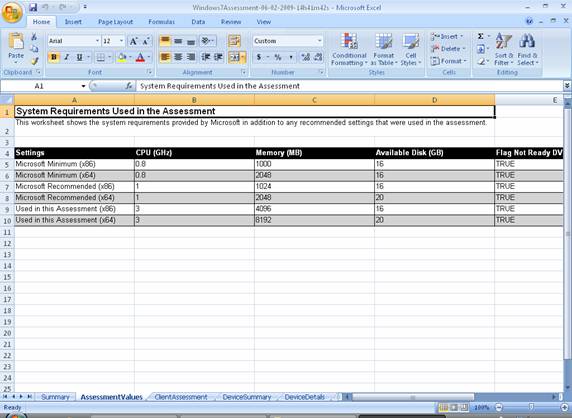
Figure 18: System Requirements Used in the Assessment worksheet
The next worksheet provides a summary of Windows 7 readiness information for computers that are already running a Microsoft Windows client operating system. For rows that report “Insufficient Data” refer to the WMI Status column for more information about why inventory data could not be collected (Figure 19):
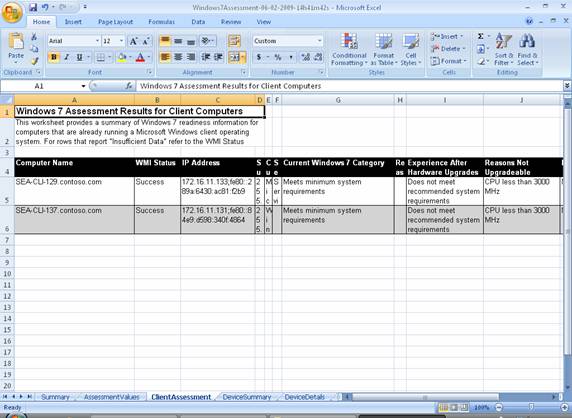
Figure 19: Windows 7 Assessment Results for Client Computers worksheet
The next worksheet is a summary of the hardware devices found on the computers. It identifies whether a driver is available on the Windows 7 DVD, from Windows Update, or if you need to contact the hardware manufacturer to identify if a driver is available for Windows 7. This summary worksheet has a row for each discovered device and provides the number of computers where the device was found. To identify the specific devices on each computer, refer to the Device Inventory Details Worksheet (Figure 20):
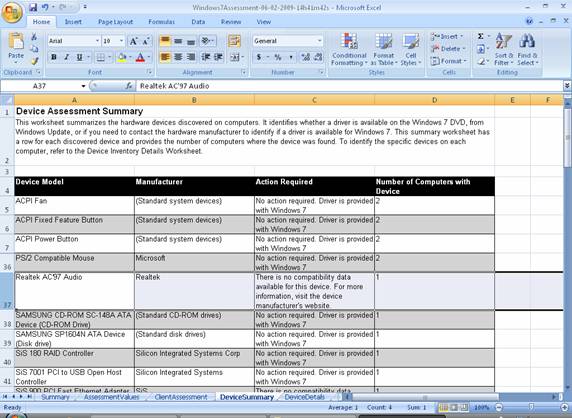
Figure 20: Device Assessment Summary worksheet
The next worksheet describes the hardware devices discovered on each specific computer. It identifies whether a driver is available on the Windows 7 DVD, from Windows Update, or if you need to contact the hardware manufacturer to identify if a driver is available for Windows 7 (Figure 21):
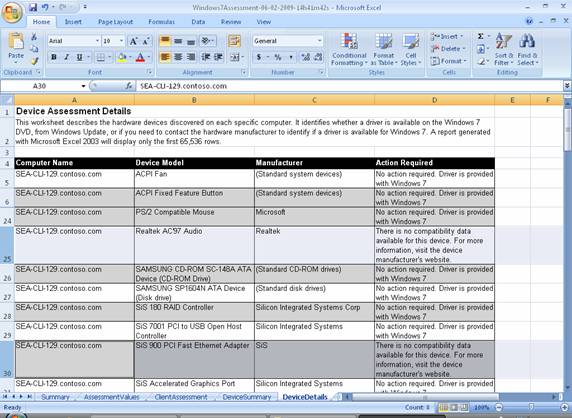
Figure 21: Device Assessment Details worksheet
The next worksheet describes computers that are not currently able to run Windows 7 and the hardware upgrades required for them to meet the minimum system requirements for Windows 7 (Figure 22):
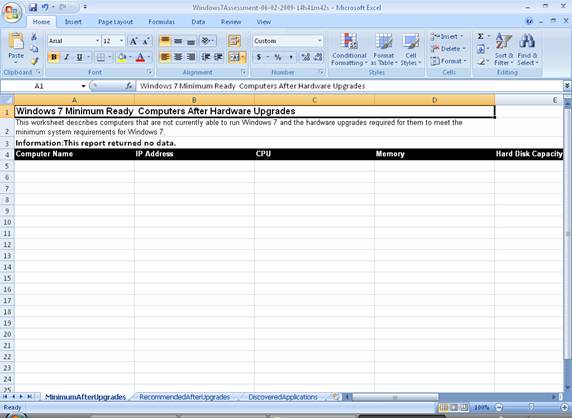
Figure 22: Windows 7 Minimum Ready Computers After Hardware Upgrades worksheet
The next worksheet describes computers that are not currently able to run Windows 7 or meet the minimum system requirements. It provides the hardware upgrades required for the computers to be ready for Windows 7 using the recommended hardware requirements selected for this assessment (Figure 23):
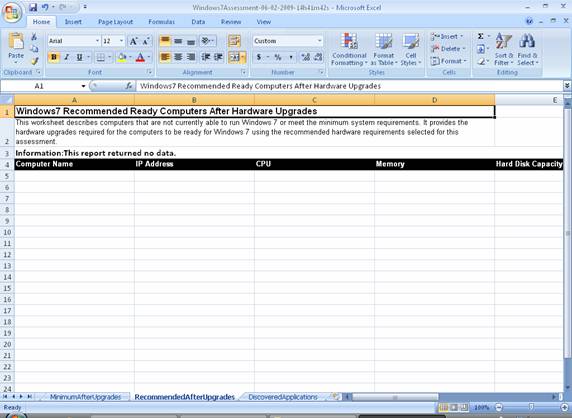
Figure 23: Windows 7 Recommended Ready Computers After Hardware Upgrades worksheet
The eighth and final worksheet describes up to 60,000 applications discovered through the inventory process on client machines and provides a count of the number of times a particular version of the software was found. The data in this sheet is based solely upon computers where a successful inventory was performed (Figure 24):
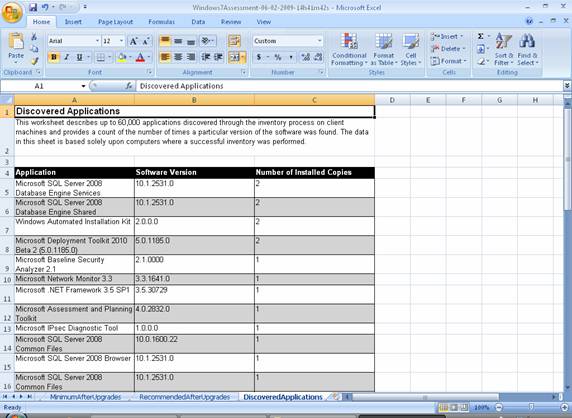
Figure 24: Discovered Applications worksheet
Finally, let us examine the Word doc generated by MAP, which summarizes the results of our Windows 7 Readiness assessment (Figure 25):
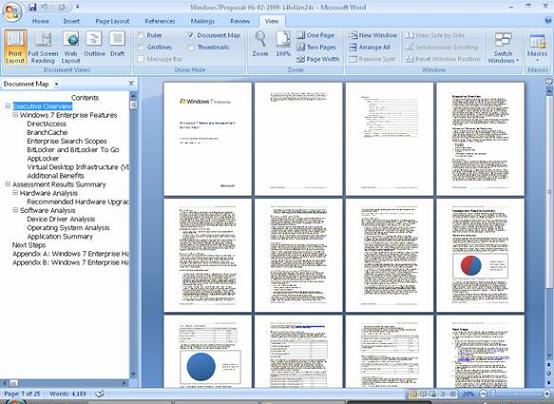
Figure 25: MAP generates a proposal you can present to management
As you can see from the outline on the left, this document contains both the results of your assessment and also some additional information concerning the benefits of deploying Windows 7 Enterprise edition in your organization. You can use this document as the basis for the proposal you will present to management. Lastly, MAP 4.0 will give you the ability to insert your own text and logos within the Word template, allowing users such as consultants to customize the outputs with their own “branding” in future scans.
Conclusion
MAP 4.0 is a powerful tool for assessing whether your desktop infrastructure is ready to migrate to Windows 7. There are other capabilities in MAP 4.0 that can help you plan a server migration and consolidation. We will examine these capabilities in a future article on this site. For more information about MAP see here on the Solution Accelerators TechCenter on Microsoft TechNet.
If you would like to read previous articles in this series, please go to:
- Deploying Windows 7 – Part 1: Windows AIK 2.0 Enhancements
- Deploying Windows 7 – Part 2: Using DISM
- Deploying Windows 7 – Part 3: Understanding MAP 4.0
- Deploying Windows 7 – Part 5: MDT 2010 Enhancements
- Deploying Windows 7 – Part 6: Lite Touch using MDT 2010
- Deploying Windows 7 – Part 7: Automated LTI Deployment
- Deploying Windows 7 – Part 8: Understanding LTI Configuration Files
- Deploying Windows 7 – Part 9: Deploying 32-bit vs. 64-bit Windows
- Deploying Windows 7 – Part 10: Capturing and Deploying an Image of a Reference Computer
- Deploying Windows 7 – Part 11: Capturing an Existing Installation
- Deploying Windows 7 – Part 12: Planning for Application Compatibility
- Deploying Windows 7 – Part 13: Manual Migration from Windows XP to Windows 7
- Deploying Windows 7 – Part 14: Automated Migration from Windows XP to Windows 7
- Deploying Windows 7 – Part 15: Configuring the MDT Database
- Deploying Windows 7 – Part 16: Using the MDT Database
- Deploying Windows 7 – Part 17: Deploying Applications Based on Make and Model
- Deploying Windows 7 – Part 18: Determining the UUID of a Computer
- Deploying Windows 7 – Part 19: Building a Custom WinPE Tools CD
- Deploying Windows 7 – Part 20: Securing MDT (Part 1)
- Deploying Windows 7 – Part 21: Securing MDT (Part 2)
- Deploying Windows 7 – Part 22: Bulk Populating the MDT Database Using PowerShell
- Deploying Windows 7 – Part 23: Managing Drivers – Introduction
- Deploying Windows 7 – Part 24: Managing Drivers – Issues and Approaches
- Deploying Windows 7 – Part 25: Managing Drivers – Selection Profiles
- Deploying Windows 7 – Part 26: Managing Drivers – By Make and Model
- Deploying Windows 7 – Part 27: Managing Drivers – Tips and Tricks
- Deploying Windows 7 – Part 28: Managing Software Updates
- Deploying Windows 7 – Part 29: Completing the LTI Deployment Infrastructure